FFTの仕組み
FFTの説明はできませんが、わたしには以下のように見えます。
(どうやら、「「定常性」があるので整数周期の基準波形との「共分散」を計算する」と言えば良いことのようです(定常と共分散)。「定常性」、「共分散」を調べてください。)
相関性の検出
マイクやスピーカーの振動板は往復運動をします。
振幅をサンプリングした数列を扱うわけですが、長い時間では、ゼロを挟んで均等に振幅しているはずです。これは、和がゼロに近づくことです。
サンプリングデータの数列があって、同じ長さの数列を乗じて和を求めることを考えて見ます。
乗じる数列が、
-
ゼロを挟んで均等に部分布する乱数列ならゼロに近づく
-
2.同じ数列なら値が大きくなる
ことは想像できます。
乗算したものの和は、相関度合いが絶対値に現れます。同符号の割合が高ければ正に、異符号の割合が高ければ負に偏ります。
| サンプリングデータと検出用の波形 |
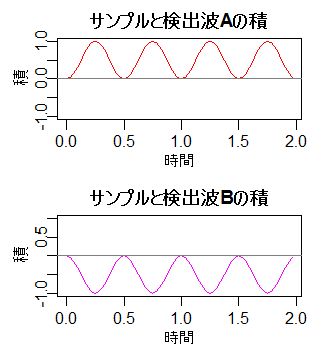 |
周期の検出

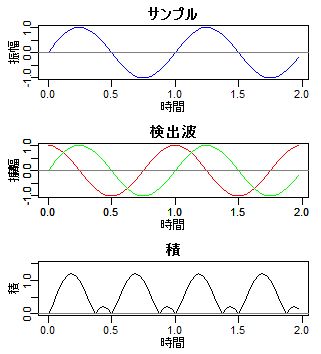
このことから、サンプリングデータの数列と同じ長さの、1周期の数列を乗じて和を求めれば1周期の周期性を検出ができます。同様に、2,3,...周期が検出ができます。
しかし、この話しには抜けがあります。
たしかに、サンプリングデータと検出波が同じ位相なら正の大きな値、πズレていれば負の大きな値になります。
しかし、左図のように、π/2 ズレている場合は、検出できません。
積は、ゼロを中心に同じだけ振幅するので、和がゼロになってしまいます。
積の和の値の絶対値は、同相なら最大で、2πずれると最小になるような周期性を持っています。
したがって、位相のπ/2ズレた検出波を2つ用意すれば解決できます。
π/2ズレるのは、sin と cos の関係なので、サンプル数がNのサンプリングデータ s[0],s[1],...,s[n-1] があるとき、
ω = 2π/n として、1周期の検出は、
F[1] = (k=0,n-1)Σ( |s[k]・(cos(kω)+sin(kω))| )
を、計算すれば位相にかかわらず、絶対値は大きな値になります。
検出に使う波形の部分は、以下のように表せます。
 cos(kpω)+sin(kpω) pは、周期を表し、0,1,...,n-1 cos(kpω)+sin(kpω) pは、周期を表し、0,1,...,n-1
また、
exp(i・x) = cos x + i・sin x
を、利用できます。
実数 x と、複素数 a+b・i の積は、
x・(a+b・i) = ax+bx・i
なので、
f[1] = (k=0,n-1)Σ( s[k]・exp(-kωi))
f[1]は、複素数で、絶対値は、
abs(a+b・i ) = √(a2+b2)
なので、相関を表す値として使えます。
n個のサンプリングデータ s[0],s[1],...,s[n-1] の FFT すると、同数の f[0],f[1],...,f[n-1] の複素数が得られます。
これは、
f[p] = (k=0,n-1)Σ( s[k]・exp(-kpωi))
を、計算したものです。
逆変換は、
s'[p] = (k=0,n-1)Σ( f[k]・exp(kpωi))
を、計算したものです。
以下は、R言語のFFTのヘルプにある例と同じことを、指数関数を乗じて計算したものです。
- > # ヘルプの例
- > x <- 1:4
- > fft(x)
- [1] 10+0i -2+2i -2+0i -2-2i
- > fft(fft(x),inverse=T)/4
- [1] 1+0i 2+0i 3+0i 4+0i
- > # FFTを計算
- > f <- rep(complex(re=0,im=0),4)
- > w <- 2*pi/4 * 1i
- > f[1] <- sum(x * c(exp(-0*0*w),exp(-0*1*w),exp(-0*2*w),exp(-0*3*w)))
- > f[2] <- sum(x * c(exp(-1*0*w),exp(-1*1*w),exp(-1*2*w),exp(-1*3*w)))
- > f[3] <- sum(x * c(exp(-2*0*w),exp(-2*1*w),exp(-2*2*w),exp(-2*3*w)))
- > f[4] <- sum(x * c(exp(-3*0*w),exp(-3*1*w),exp(-3*2*w),exp(-3*3*w)))
- > f
- [1] 10+0i -2+2i -2-0i -2-2i
- > # 逆変換
- > s <- rep(complex(re=0,im=0),4)
- > s[1] <- sum(f * c(exp(0*0*w),exp(0*1*w),exp(0*2*w),exp(0*3*w)))
- > s[2] <- sum(f * c(exp(1*0*w),exp(1*1*w),exp(1*2*w),exp(1*3*w)))
- > s[3] <- sum(f * c(exp(2*0*w),exp(2*1*w),exp(2*2*w),exp(2*3*w)))
- > s[4] <- sum(f * c(exp(3*0*w),exp(3*1*w),exp(3*2*w),exp(3*3*w)))
- > round(s/4,3)
- [1] 1+0i 2+0i 3+0i 4+0i
振幅のレンジ
サンプルはゼロを中心にした振幅値ですが、16ビットの整数型なら[-32768,32767],32ビットの浮動小数点なら[-1,1]の値を取ります。
また、サンプリング時の音量で、データのレンジは変わります。
検出のための数列は、[-1,1]です。
計算は同じ長さの数列の積の和を求めているので、算出される値は、サンプルのレンジとサンプル数に依存しています。
FFTの計算自体は、サンプルのレンジにかかわらず可能ですが、算出値を使う上では注意が必要です。
検出波形と位相

検出波形は、常にゼロ度から始まっています。
サンプルの位相はいろいろです。
32サンプルで1周期のサインカーブのデータを作ります。
データを作る際に、開始の角度を[-π,π]でずらして、どう検出されているかを見て見ます。
FFTの計算結果の1周期に当たる、ゼロから数えて1番目の値は、左図のようです。
左図の青い線は、絶対値です。位相がズレても周期を同じ値(16)と検出しています。
32サンプルで、積の和を計算しているので32が1周期のパワーです。ペアを成す31番目の値との和が32になります。
赤が偏角です。
FFTの計算に使われる検出用の波形は、常に角度がゼロから計算されます。
これは、 exp(-x・i) = cos x - i・sin x です。
cos と sin の波形は位相がπ/2ズレている波形です。
実部の絶対値が大きいのは、ゼロから計算されたcosカーブとの相関が高いことを示しています。
虚部の絶対値が大きいのは、ゼロから計算されたsinカーブとの相関が高いことを示しています。
もう少し詳細に
サンプル数が N の場合、0からN-1周期までの整数周期の検出波形を使って、相関度合を調べるのがFFTです。
FFTの計算は、周期によらず、一様な計算をします。
しかし、検出波形の周期性から、算出値は、3つ、または4つの部分に分けられます。
ゼロ周期
FFTの結果の先頭は、検出波形を作る指数関数の引数がすべてゼロの場合で、すべて1を乗じた和が計算されることになります。
したがって、この値の虚部は常にゼロになります。
サンプリングデータは、ゼロを中心に振幅しているので、この値はゼロに近づきます。
もし、ゼロでないなら、振幅に偏りがあることを意味し、直流成分と解釈されます。
Nが偶数の場合のN/2+1番目の値
ナイキスト周波数(N/2周期)に当たる、この周期は、検出波形を作る指数関数の引数が、0 と π の繰り返しで、指数関数は 1,-1、… となります。
したがって、この値の虚部は常にゼロになります。
「Nが偶数の場合のN/2+1番目」と、ゼロ周期を除いた前半
普通にスペクトルを表す値です。後述の「Nが偶数の場合のN/2+1番目について」のように2倍して扱われます。
「Nが偶数の場合のN/2+1番目」と、ゼロ周期を除いた後半
計算自体は、周波数の高い値を計算していますが、後述の「Nが偶数の場合のN/2+1番目について」のように指数関数(三角関数)の性質から前半と同じ周期の検出値となります。
前半とは共役数の関係にあるので通常使う必要がありません。(計算の必要もありません。)
Nが偶数の場合のN/2+1番目について
下のスクリプトの実行結果は、8サンプルで1周期と4周期の正弦波を合成した波形で、以下のことを表そうとするものです。
-
「Nが偶数の場合のN/2+1番目」に相当する4周期は、サンプリングのタイミングによっては全く検出されない。
-
「Nが偶数の場合のN/2+1番目」に相当する4周期は、サンプリングのタイミングによって算出値が変わる。
-
「Nが偶数の場合のN/2+1番目」に相当する4周期以外は、サンプリングのタイミングによって算出値が変わらない。
-
「Nが偶数の場合のN/2+1番目」に相当する4周期は、値が最大2倍になる。
- > # 8サンプルで1周期と4周期の正弦波
- > t <- seq(0,by=1/8,length=8)
- > s <- (sin(2*pi*1*t) + sin(2*pi*4*t)) / 2
- > # 初期位相ゼロ(開始サンプリング時刻が角度ゼロ)の場合の、
- > # 8サンプルで4周期の正弦波のサンプリング値
- > round(sin(2*pi*4*t),3)
- [1] 0 0 0 0 0 0 0 0
- > # したがって、FFTで4周期は検出されない
- > round(fft(s),3) # FFTの結果
- [1] 0+0i 0-2i 0+0i 0+0i 0+0i 0+0i 0+0i 0+2i
- > # 4周期の初期位相をずらせば(サンプリングのタイミングをずらせば)
- > # 検出される(π/3ずらしてみる)
- > s <- (sin(2*pi*1*t +pi/3) + sin(2*pi*4*t +pi/3)) / 2
- > round(fft(s),3) # FFTの結果
- [1] 0.000+0i 1.732-1i 0.000+0i 0.000+0i 3.464+0i 0.000+0i 0.000+0i 1.732+1i
- > round(Re(fft(s)*Conj(fft(s))),3) # パワー
- [1] 0 4 0 0 12 0 0 4
- > # π/2ずらす
- > s <- (sin(2*pi*1*t +pi/2) + sin(2*pi*4*t +pi/2)) / 2
- > round(fft(s),3)
- [1] 0+0i 2+0i 0+0i 0+0i 4+0i 0+0i 0+0i 2+0i
- > round(Re(fft(s)*Conj(fft(s))),3) # パワー
- [1] 0 4 0 0 16 0 0 4
「Nが偶数の場合のN/2+1番目」は、検出波形を作る指数関数の引数が 0 と π の繰り返しとなります。
したがって、検出波形のsin 側は常にゼロとなります。cos 側が、1、-1、… となり、大きさとしてはサンプリング値がそのまま反映されます。
「Nが偶数の場合のN/2+1番目」の周期のサンプリング値は、すべて絶対値が等しく、符号が交互しています。絶対値は、サンプリングのタイミングで変わります。
「Nが偶数の場合のN/2+1番目と、ゼロ周期」以外は、sin と cos の2つの検出波形が機能します。この2つの波形は位相がπ/2ずれた同じ波形です。
一方との相関が高ければ、他方は低くなると言うことになるので、合わせた大きさを見れば、サンプリングのタイミングの影響が相殺されています。

「Nが偶数の場合のN/2+1番目と、ゼロ周期」以外の、FFTが算出する値の大きさを、サンプリングデータが[-1,1]に正規化されているとして考えます。
まず、1つの波形の検出する値の最大値を考えます。
サンプリングデータと検出波形の周期と位相が同じときに最大になるので、単に等間隔に計算した sin の値の2乗を合算します。
n 周期の最大値 f(n) は、

となります。n、k は、共に0からN-1の整数です。
cos の計算は、整数回の回転の和で、この値は常にゼロになります。(図のように、等間隔の1周分の和は、サンプル数によらず左右対称で、合計はゼロになる。)
したがって、N/2 が最大値になります。
次に、指数関数は2つの検出波形を作りますが、これを考慮します。この関係は、一方との相関が高ければ、他方は低くなると言うもので、最大は N/2 です。
さらに、前半と後半の共役ペアについて考えます。
「1周期とN-1周期」、「2周期とN-2周期」、… は、同じ周期の検出波形になります。
これらは、「Nが偶数の場合のN/2+1番目と、ゼロ周期」以外は、FFTの算出値の2か所に、同じ周期の検出結果があることを示しています。
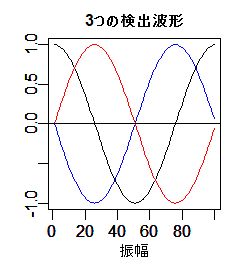
- N <- 100 # ポイント数
- w <- 2*pi/N # ポイント数で1周
- E1 <- exp(-(1i)*w*1*(0:(N-1))) # 1周期
- E2 <- exp(-(1i)*w*(N-1)*(0:(N-1)))# N-1周期
- # プロット
- plot(Re(E1),type="l",xlab="振幅",ylab="")
- par(new=TRUE)
- plot(Im(E1),type="l",col="blue",xlab="",ylab="")
- par(new=TRUE)
- plot(Re(E2),type="l",xlab="",ylab="")
- par(new=TRUE)
- plot(Im(E2),type="l",col="red",xlab="",ylab="")
- abline(h=0)
- title("3つの検出波形",cex.main=1)
このことは3通りの位相で検出を行うことです。図は、前半と後半の2か所の1周期の検出波形を描いています。
この2か所は、実数部(cos)は同じで、虚数部(sin)は符号が逆になっています。両者は、sinとの相関度の符号が反転する以外は全く同じ値を検出することになります。
「Nが偶数の場合のN/2+1番目と、ゼロ周期」以外の箇所の最大は N/2 となります。
「Nが偶数の場合のN/2+1番目と、ゼロ周期」については、サンプル数 N が最大値になります。これは、乗じる指数関数の値の絶対値がすべて1であるためです。
これが、「Nが偶数の場合のN/2+1番目と、ゼロ周期」以外を、2倍して扱う理由のようです。ペアを成す値を合計すると言うよりは、単にスケールを合わせることが目的のようです。
(FFTは本来、三角関数による近似式の係数を求めるもので、その場合は、FFTの結果の後半部分も使われます。その意味でペアの合計と言うのも当たっています。)
ゼロ詰めすると成り立たない
「Nが偶数の場合のN/2+1番目と、ゼロ周期」以外の箇所の最大は N/2 と言うことはゼロ詰めしてFFTを計算すると成り立ちません。
(1,2,4周期の大きさがそれぞれ1となると言う意味で、合成したサンプリングデータは[-1,1]になっていません。)
- > # 8サンプルで1周期と2周期、4周期の余弦波
- > t <- seq(0,by=1/8,length=8)
- > s <- cos(2*pi*1*t) + cos(2*pi*2*t) + cos(2*pi*4*t)
- > f <- fft(s) # FFT
- > round(f[1:5],2) # ゼロ詰めなし
- [1] 0+0i 4+0i 4+0i 0+0i 8+0i
- > f <- fft(c(s,rep(0,8)))# ゼロ詰めしてFFT
- > round(f[1:9],2)
- [1] 0+0.00i 3+2.38i 4+0.00i 3+0.23i 4+0.00i 3-1.77i 0+0.00i 3+4.38i 8+0.00i
8サンプルをゼロ詰めで16サンプルにしてFFTを計算すると、「Nが偶数の場合のN/2+1番目」だけでなく、N/2番目も N/2 以上の大きさになります。
ゼロ詰しない場合のN/2周期は3周期で、ゼロ詰した場合のN/2周期は7周期です。このFFTは以下のように計算されます。
- > # 8サンプルで1周期と2周期、4周期の余弦波
- > t <- seq(0,by=1/8,length=8)
- > s <- cos(2*pi*1*t) + cos(2*pi*2*t) + cos(2*pi*4*t)
- > # ゼロ詰めなしのN/2周期の計算
- > E1 <- exp(-(1i)*(2*pi/8)*3*(0:7))
- > round(s %*% E1,3)
- [1,] 0+0i
- > # ゼロ詰めした場合の、N/2周期の計算
- > E2 <- exp(-(1i)*(2*pi/16)*7*(0:15))
- > round(c(s,rep(0,8)) %*% E2,3)
- [1,] 3+4.378i
この差が何から来るのか見て見ます。
下図左は、ゼロ詰なしの3周期の計算です。サンプリングデータと検出用の波形(cos,sin)の積が、赤と青の線です。
赤も青も合計すると正負で相殺され合計がゼロになり、FFTの計算結果の実部も虚部もゼロになります。
下図右は、8個のゼロを付加して16サンプルでFFTを計算する場合の7周期の計算です。左図と同じ基準では、3.5周期に相当します。
赤も青、正に偏っており、合計がゼロになりません。
 ゼロ詰めではなく、16サンプルサンプリングしたとすると左図のようになり、正負相殺してゼロになります。 ゼロ詰めではなく、16サンプルサンプリングしたとすると左図のようになり、正負相殺してゼロになります。
ゼロ詰めした結果の奇数周期は、正しく検出されないと考えて良さそうです。
「ゼロ詰め」参照。 |